In questo articolo trovi le formule della sfera che ti servono per i compiti in classe di geometria alle scuole secondarie di I e II grado, ma anche per rispondere ai quiz di matematica del test di medicina e odontoiatria, veterinaria, professioni sanitarie.
Però, prima di vedere le formule è importante capire cos’è la sfera, da quali parti è composta e quali sono le sue proprietà principali.
In più, guarda il video con la teoria, le immagini e gli esercizi sulla sfera svolti dal nostro tutor di matematica.
Definizione di sfera
In geometria si danno almeno 2 definizioni di sfera:
la sfera è il solido formato da un insieme di punti dello spazio la cui distanza da un punto fisso, detto centro della sfera, è uguale o minore a una lunghezza costante, detta raggio della sfera.
Oppure, la sfera può essere definita come:
il solido che si ricava facendo ruotare un semicerchio intorno al suo diametro.
Parti della sfera
Ecco le parti principali della sfera:
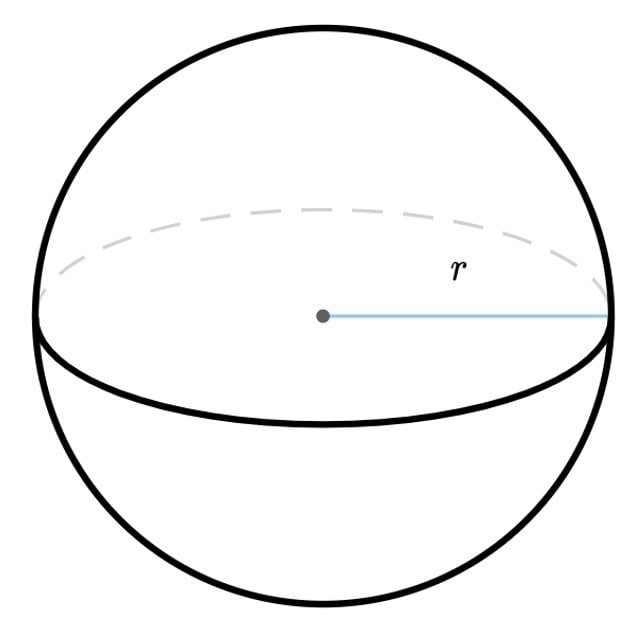
- raggio della sfera, ogni segmento che congiunge un qualsiasi punto della superficie della sfera con il centro della sfera stessa;
- superficie della sfera, l’insieme dei punti dello spazio che sono equidistanti dal centro della sfera e hanno distanza pari al raggio della sfera stessa;
- calotta sferica, ciascuna delle sezioni in cui la sfera è divisa da un piano secante. Se il piano secante passa per il diametro, le calotte sferiche prendono il nome di emisferi;
- settore sferico, la sezione della sfera delimitata dalla superficie laterale di un cono retto con vertice nel centro della sfera e dalla superficie laterale di una calotta sferica.
- fuso sferico, la porzione di superficie sferica compresa tra due semicerchi che hanno lo stesso diametro;
- spicchio sferico, la sezione della sfera compresa tra due semicerchi aventi identico diametro.
Proprietà della sfera
La sfera ha tante e importanti proprietà. Tuttavia, alcune vengono studiate solo alle scuole superiori, altre all’università, perché troppo complesse da dimostrare. Qui ti indichiamo le 3 principali proprietà della sfera:
- la sfera è il solido che si caratterizza per avere il minimo rapporto tra superficie e volume;
- la sfera è il solido più simmetrico perché ha simmetria centrale (perché simmetrica rispetto al centro) e conta infiniti assi di simmetria;
- dato un cilindro circoscritto a una sfera, il volume del cilindro è pari a 3/2 quello della sfera mentre la sua superficie laterale è uguale a quella della sfera stessa.
Formule sfera
Vediamo ora le formule della sfera necessarie per capire come si calcola il volume della sfera, l’area, la superficie e tutto il resto. Ricorda che da ognuna di queste formule puoi ricavare la relativa formula inversa.
Premesso che Pi Greco (π) è un valore costante approssimato π≃3,14, ecco l’elenco delle formule della sfera:
- circonferenza → C = 2πr
- raggio (formula inversa della circonferenza) → r = C/2π
- diametro → d = 2r
- raggio (formula inversa del diametro) → r = d/2
- volume → V = 4/3πr3
- raggio (formula inversa del volume) → r = 3√(3V/4π)
- superficie totale della sfera → Stot = 4πr2
- raggio (formula inversa della superficie totale) → r = √(Stot/4π)
- area del cerchio equatoriale → Ae = πr2
- raggio (formula inversa dell’area del cerchio equatoriale) → r = √(Ae/ π)
- perimetro equatoriale → 2pe = 2πr
- superficie della calotta sferica → S = 2πrh
- volume della calotta sferica → V = πh2 ∙ (r – h/3)
- superficie del settore sferico → S = πr ∙ (r + 2h)
- volume del settore sferico → V = 2/3πr2h
- superficie del fuso sferico → S = (απr2/90°)
- volume dello spicchio sferico → V = (απr3/270°)
Ora che conosci teoria e formule, guarda il video con gli esercizi sulla sfera svolti dal nostro tutor di matematica.
Video e immagine nel testo di Marco Ogana, tutor WAU!
Immagine in evidenza di Michael L. da Pexels

