Le formule sul moto circolare uniforme e la teoria su questa tipologia di moto sono tra gli argomenti fondamentali della fisica.
Infatti, il moto circolare uniforme è un argomento che capita di frequente sia in compiti in classe e interrogazioni alle scuole superiori sia nei quiz del test di medicina, veterinaria e professioni sanitarie.
In questo articolo troverai tutte le formule e le definizioni. In più, la videolezione sul moto circolare uniforme con un esercizio spiegato della nostra tutor di fisica.
Moto circolare uniforme: definizione
Che cos’è il moto circolare uniforme?
Nel MUC, Moto Circolare Uniforme, un corpo si muove lungo una circonferenza a velocità costante in modulo, ma non in verso e direzione.
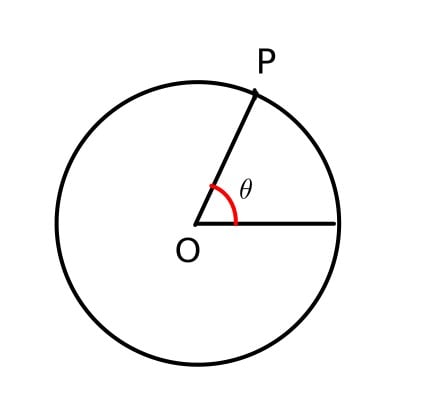
Possiamo dare anche un’altra definizione. Dato un punto P sulla circonferenza, questo punto percorrerà spazi uguali in eguali intervalli di tempo.
Il moto circolare uniforme è importante perché spesso può essere usato per descrivere il movimento di tanti corpi che si muovono intorno a noi, come quello di un sasso legato a una corda che viene fatto roteare o quello di una giostra.
Formule moto circolare uniforme
Ecco un elenco delle formule del moto circolare uniforme. Continua a leggere perché a seguire troverai la relativa spiegazione.
- velocità tangenziale v = 2πr/T e periodo T = 2πr/v
- velocità angolare ω = 2π/T e periodo T = 2π/ω
- frequenza ƒ = 1/T
- accelerazione: ac = v2/r = ω2r
- legge oraria θ(t) = θ0 + ωt
Velocità tangenziale moto circolare uniforme
Nel moto circolare uniforme abbiamo due tipi di velocità:
- la velocità tangenziale
- la velocità angolare
Cosa occorre per definire la velocità nel moto circolare uniforme?
La velocità tangenziale nel moto circolare uniforme è costante ed esprime la quantità di spazio che il punto P percorre in un determinato arco di tempo.
Ricordiamo che è costante solo in modulo, non in verso e direzione. Il verso è quello in cui viene percorsa la traiettoria, orario o antiorario. La direzione è quella della retta tangente alla circonferenza nel punto P.
Per cui la formula della velocità tangenziale, intesa come rapporto tra spazio percorso e tempo per percorrerlo, ossia tra circonferenza e intervallo di tempo costante, sarà:
v = 2πr/T dove T è chiamato periodo.
Periodo moto circolare uniforme
Come abbiamo detto, la velocità nel moto circolare uniforme è costante. Quindi il punto P impiegherà sempre lo stesso tempo per percorrere la circonferenza. Ecco perché il tempo T prende il nome di periodo.
Il periodo è il tempo impiegato a percorre un giro e si misura in secondi.
Come calcolare T nel moto circolare uniforme? Basta applicare la formula inversa della velocità tangenziale, ossia:
T = 2πr/v
Velocità angolare nel moto circolare uniforme
La velocità angolare, detta ω (omega), è il rapporto tra l’angolo descritto da P nel suo moto e il tempo impiegato a descriverlo.
Poiché la velocità è costante, tale angolo sarà un angolo completo di 360°, espresso in radianti.
Quindi, la formula della velocità angolare sarà:
ω = 2π/T
La formula inversa del periodo sarà T = 2π/ ω.
Per cui, ricapitolando, poiché v = 2πr/T mentre ω = 2π/T, possiamo dire che la velocità tangenziale dipende dal raggio, a differenza della velocità angolare. Infatti, sostituendo la formula della velocità angolare in quella della velocità tangenziale otteniamo che:
v = ωr
Moto circolare uniforme: la frequenza
La frequenza è il numero di eventi che avvengono in un secondo. La frequenza è espressa in 1/s oppure Hz, Hertz. Ma può anche essere espressa come giri al minuto o in altri modi.
La frequenza non va confusa con il periodo, di cui è il reciproco.
Per cui, la formula della frequenza nel moto circolare uniforme è:
ƒ = 1/T.
Accelerazione centripeta moto circolare uniforme
Ricorda che nel moto circolare uniforme la velocità è costante solo in modulo. Questo significa che per modificare la direzione del moto lungo la circonferenza deve esserci una accelerazione, detta appunto accelerazione centripeta perché tende verso il centro e forma un angolo di 90° con la velocità:
ac = v2/r = ω2r
Come varia l’accelerazione centripeta al variare del raggio?
Data questa formula possiamo affermare che anche la accelerazione centripeta è costante in modulo se il raggio rimane costante e aumenta al diminuire del raggio e viceversa.
Legge oraria moto circolare uniforme
Infine, la formula della legge oraria del moto circolare uniforme, cioè l’equazione che descrive questo specifico tipo di moto e permette di definire la posizione in funzione del tempo, è:
θ(t) = θ0 + ωt
La legge oraria del moto circolare uniforme è simile a quella del moto rettilineo uniforme. Le differenze tra le legge oraria del moto circolare uniforme e del moto rettilineo uniforme sono:
- la posizione iniziale e al tempo t è espressa con theta ossia l’angolo, poiché siamo su una circonferenza;
- al posto della velocità tangenziale c’è la velocità angolare ω.
Non ricordi cos’è il moto circolare uniforme? Vai a Moto rettilineo: leggi orarie, formule, esercizi.
Per approfondire, guarda la videolezione con la teoria, le formule e un esercizio sul moto circolare uniforme svolto dalla nostra tutor di fisica.
Video e immagini nel testo di Eleonora Parlanti, tutor WAU!
Immagine in evidenza di Sanndy Anghan da Pexels



