Il piano cartesiano online: tutto quello che devi sapere sul piano cartesiano se sei uno studente delle scuole superiori oppure ti stai preparando per i test di ammissione a medicina, professioni sanitarie, veterinaria.
Cos’è il piano cartesiano?
Il piano cartesiano è un sistema di riferimento formato da due rette ortogonali. Nel piano cartesiano le due rette ortogonali orientate e definite da una unità di misura o metrica, si intersecano in una origine.
Su questo sistema di rette, puoi individuare i punti, mediante una coppia di numeri reali detta coordinate cartesiane, il cui valore è chiamato ascissa e ordinata, e rappresentare qualsiasi figura geometrica piana.
In generale, un sistema di riferimento cartesiano è qualsiasi sistema formato da n rette ortogonali che si intersecano in una origine, orientate e misurabili.
La definizione di piano cartesiano
Come si rappresenta il piano cartesiano
Per disegnare il piano cartesiano devi tracciare due linee rette perpendicolari e orientate, di solito una è orizzontale e l’altra verticale. Queste due rette sono chiamate assi cartesiani, più precisamente:
- la retta orizzontale è detta asse delle ascisse o asse delle x
- la retta verticale è detta asse delle ordinate o asse delle y
Per questo motivo, il piano cartesiano è anche conosciuto come il piano xy.
Come rappresentare il piano cartesianoCome funziona il piano cartesiano
Le due rette intersecandosi formano 4 quadranti, identificati da numeri romani progressivi ordinati in senso antiorario.
I quadranti del piano cartesiano sono:
- I quadrante, i cui punti hanno tutti ascissa e ordinata positive;
- II quadrante, i cui punti hanno ascissa negativa e ordinata positiva;
- III quadrante, i cui punti hanno tutti ascissa e ordinata negative;
- IV quadrante, i cui punti hanno ascissa positiva e ordinata negativa.
Attraverso il sistema della coppia dei due assi, ogni punto del piano può essere individuato da una coppia di numeri reali: le coordinate nel piano cartesiano.
Le coordinate cartesiane in valore assoluto rappresentano la distanza del punto rispettivamente dall’asse x e dall’asse y.
Genericamente le coordinate di un punto sono indicate come (x;y):
- i punti sull’asse x hanno tutti ordinata y=0
- i punti sull’asse y hanno tutti ascissa x=0
- le coordinate cartesiane dell’origine sono x=0 e y=0.
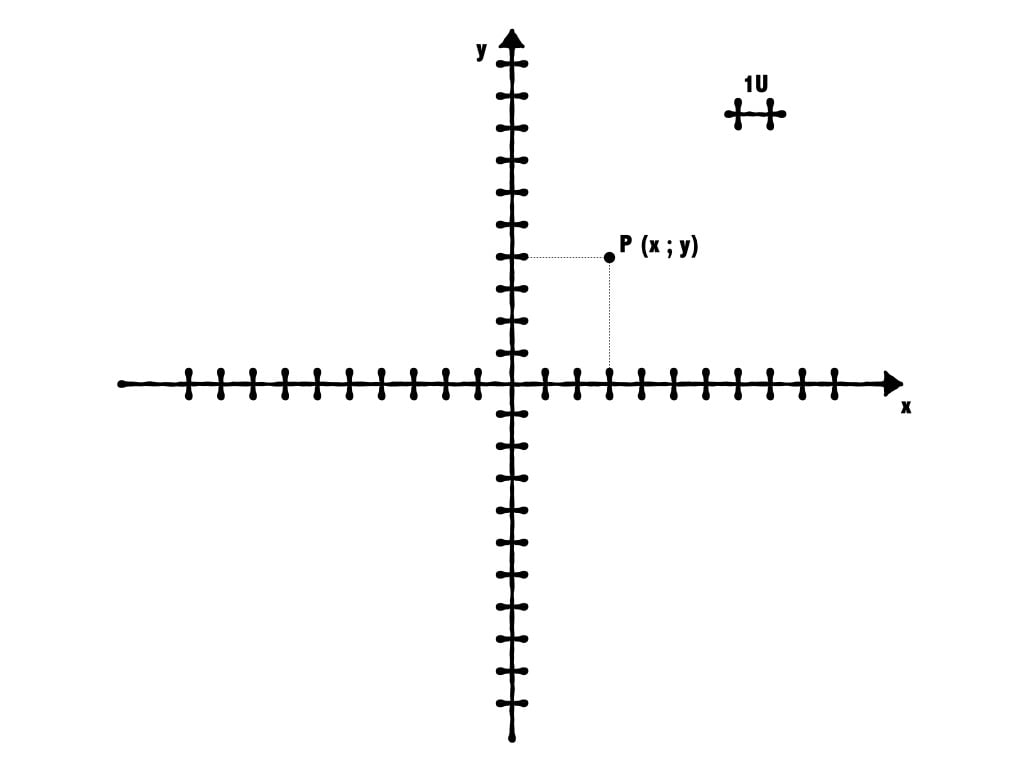Piano cartesiano ascisse e ordinate
Punti nel piano cartesiano
Piano cartesiano: le equazioni
Inoltre, il piano cartesiano consente di rappresentare graficamente funzioni di equazione, con x variabile indipendente e y dipendente.
y = ƒ(x)
Da questa formula, si ricava che:
- l’equazione dell’asse delle ascisse è y=0
- l’equazione dell’asse delle ordinate è x=0
- l’equazione di una retta perpendicolare all’asse delle ascisse è y=K
- l’equazione di una retta perpendicolare all’asse delle ordinate è x=K
La retta nel piano cartesiano
L’equazione della retta è:
y = mx + q
Questa è la forma esplicita, dove m è il coefficiente angolare dato da Δy/Δx.
m indica l’inclinazione della retta ovvero l’angolo che la retta forma con il semiasse positivo delle ascisse.
Come si legge sull’Enciclopedia Treccani:
“Il coefficiente angolare è positivo se e solo se la retta è crescente (nella direzione delle x crescenti), negativo se e solo se la retta è decrescente, nullo se la retta è parallela all’asse delle ascisse (e rappresenta perciò una funzione costante).”
L’equazione di una retta può essere espressa anche in forma implicita, ad esempio:
ax + by + c = 0
Studia meglio la retta. Vai a La retta: cos’è, formule ed esercizi. Trovi anche una videolezione con disegni ed esercizi svolti sulla retta dal nostro tutor.
Come calcolare la distanza fra due punti sul piano cartesiano
Il teorema di Pitagora nel piano cartesiano
Misurare la distanza fra due punti in un piano cartesiano è molto semplice se i due punti hanno stessa ordinata o stessa ascissa.
In entrambi i casi, una volta scelta l’unità uguale a un quadratino, basterà contare i quadratini che separano un punto da un altro.
La formula da utilizzare nel caso in cui due punti A e B abbiano la stessa y è:
Δx = |xA – xB|
La formula da utilizzare nel caso in cui due punti B e C abbiano stessa x è:
Δy = |yB – yC|
Tutto ciò è mostrato nell’immagine qui sopra.
Il problema si complica un poco nel caso in cui entrambe le coordinate dei due punti, A e C, siano diverse: qui sarà necessario utilizzare il Teorema di Pitagora.
AC2 = (xA – xC) 2 + (yA – yC) 2 = Δx2AC + Δy2AC
La radice quadrata di AC ci darà la distanza fra questi punti.
Guarda su YouTube la nostra breve videolezione sul piano cartesiano con lo svolgimento di un esercizio su come calcolare la distanza fra due punti e l’applicazione del Teorema di Pitagora nel piano cartesiano per risolvere un problema sul triangolo.
La storia del piano cartesiano
Conoscere la storia di un argomento, può aiutarti a fissarlo meglio nella memoria. Leggi questi brevi cenni su come si è arrivati al concetto di piano cartesiano.
La nozione di coordinate geometriche è stata introdotta per la prima volta da Nicola d’Oresme, matematico vissuto nel XIV secolo.
Tuttavia, il nome del piano cartesiano deriva dal cognome di René Descartes, che forse conosci meglio come Cartesio, filosofo e matematico francese, che in due suoi scritti del 1637 mise insieme gli studi di algebra e quelli di geometria euclidea.
Immagine in evidenza Gerd Altmann da Pixabay
Disegni nel testo del Dott. Luca Nuvoli
